Dezibel Tutorial: dB und dBm vs. Gain und Milliwatt

Das Konzept eines Dezibels (dB) ist verständlicherweise schwierig und verwirrend für jemanden, der es gerade erst kennenlernt. Das Kombinieren von Spezifikationen für Verstärkung, Leistung und Spannung (und Stromstärke, aber nicht so häufig), die dB, dBm, dBW, Watt, Milliwatt, Spannung, Millivolt usw. mischen, erfordert häufig das Umrechnen zwischen linearen Werten und Dezibelwerten. Dieses kurze Tutorial soll helfen, den Unterschied zwischen der Arbeit mit Dezibel und der Arbeit mit linearen Werten zu verdeutlichen.

Logarithmen (Logs) wurden erstmals in den frühen 1600s vom schottischen Mathematiker John Napier als Werkzeug zur Vereinfachung von Multiplikations- und Divisionsoperationen konzipiert, indem sie in schnellere und weniger fehleranfällige Additions- bzw. Subtraktionsoperationen umgewandelt wurden. Dies wird ermöglicht, weil die Multiplikation von zwei Zahlen, die als ähnliche Basiszahlen mit Exponenten ausgedrückt werden, durch bloßes Addieren der Exponenten erreicht werden kann. Die Division dieser gleichen Zahlen erfolgt durch Subtrahieren der Exponenten. Es ist eines der Gesetze der Exponenten und sieht so aus:

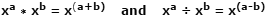
Verwenden Sie als Beispiel tatsächliche Zahlen mit x = 10, a = 4, b = 1:

Das Gesetz der Exponenten gilt für jede Basiszahl, nicht nur für 10. Nämlich:

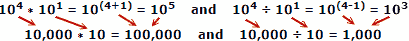
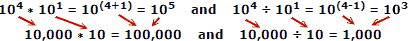
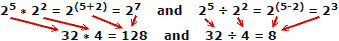
Menschen neigen dazu, beim Addieren und Subtrahieren von Zahlen weniger Fehler zu machen, so dass der Vorteil von Logarithmen offensichtlich ist. Denken Sie daran, dass Logarithmen entwickelt wurden, bevor automatische mechanische oder elektronische Computer zur Verfügung standen. Ein Rechenschieber nutzt die Eigenschaften von Logarithmen zur Berechnung aus, dies ist jedoch ein separates Hauptthema.

Dies sind einfache Beispiele, gelten jedoch für jede Basis oder jeden Exponenten. In Abwesenheit eines Taschenrechners benötigen Sie eine Zahlentabelle und ihre entsprechenden Logarithmen, um für die allgemeine Anwendung nützlich zu sein. Frühe Protokolltabellen füllten Volumes, abhängig vom Abstand zwischen Zahlen (1.000, 1.001, 1.002, 1.003 vs. 1.0, 1.1, 1.2, 1.3 usw.). Die gute Nachricht für Entwickler von Logarithmentabellen ist, dass nur ein einziges 'Jahrzehnt' von Zahlen (z. B. 1 bis 10) erforderlich ist, da jedes vorangegangene oder nachfolgende Jahrzehnt ein einfaches Vielfaches einer Potenz von 10 ist.

Hinweis: In dieser Diskussion verwende ich Basis-10, da dies die Basis unseres gemeinsamen Zahlensystems ist - daher der Begriff "gemeinsamer Logarithmus" für Basis-10-Protokolle. Möglicherweise haben Sie von natürlichen Logarithmen gehört, bei denen die Basis von e verwendet wird, aber e wird bei der Berechnung von skalarer elektrischer Leistung, Spannung und Stromstärke nicht sehr häufig verwendet (obwohl es verwendet wird, wenn Phasenwinkel, dh die Euler-Identität, enthalten sind). Natürliche Logarithmen werden als ln (x) ohne den Index 'e' geschrieben, wohingegen Basis-10-Logarithmen normalerweise einfach als log (x) ohne den Index 10 geschrieben werden. dh nicht loge (x) oder log10 (x).

Pro Basis = 10-Protokolltabelle:

Semi-Logarithmische 5-Zyklen Technisches Millimeterpapier - RF Cafe Die Ausnahme und der Sonderfall ist logx (0) = Undefiniert. Das liegt daran, dass es keine Potenz gibt, mit der Sie eine beliebige Zahl erhöhen und 0 (Null) erhalten können. Sie können asymptotisch gegen Null gehen, aber nicht gegen Null. Auf einer Log-Skala wird niemals die Zahl Null angezeigt. Sie laufen normalerweise von einer Potenz von 10 zu einer anderen Potenz von zehn. Ein Beispiel für Millimeterpapier ist rechts abgebildet. Es hat 5 "Zyklen" oder "Jahrzehnte" Reichweite. Beachten Sie, dass es auf der y-Achse keine Null gibt.

Der Basis-10-Logarithmus (allgemeiner Logarithmus) einer Zahl ist dann der Exponent, auf den 10 angehoben werden muss, um diese Zahl zu erhalten. Mit anderen Worten ist das Basis-10-Protokoll von 2 100 (log102 100 = 10), da 100 gleich 2 ist (log10 100 = 2).

Dies ist das Grundgesetz der Logarithmen:


Durchführen derselben Multiplikationen und Divisionen wie oben auf der Seite unter Verwendung tatsächlicher Logarithmen:



Das ist in Ordnung, aber am Ende erhalten Sie den Logarithmus der gesuchten Zahl. Frage: Wie erhalten Sie, abgesehen von einem einfachen Beispiel wie diesem, die Antwort, die Sie benötigen? Antwort: Schlagen Sie den Antilogarithmus (Antilog) des Ergebnisses nach. In diesem Fall:

Ein härteres und wahrscheinlicheres Beispiel mit Zahlen, die keine ganzzahligen Potenzen von 10 sind, könnte ungefähr so ​​aussehen:




 HP-35-Rechner (Wikipedia) - RF CafeSeit der Logarithmus von 'x' gleich 1.8444 ist, ist der Antilog gleich 'x', was 69.9 ist



Ich habe meinen Taschenrechner verwendet, um die Protokolle und Antilogs nach diesen Zahlen zu durchsuchen, aber vor 1972, als Hewlett Packard (HP) den wissenschaftlichen Taschenrechner HP-35 einführte, brauchte die durchschnittliche Person keinen Zugriff auf einen Unternehmens- oder Universitäts-Großrechner, um ein Protokoll zu verwenden Tabelle, um solche Berechnungen durchzuführen.

Wer stört sich heute daran, Logarithmen zu verwenden? Viele Leute, auch ich, berechnen häufig kaskadierte Systemparameter wie Rauschzahl (NF) und Schnittpunkte (IP). Einfaches Addieren und Subtrahieren von Gain-dB- und Power-dBm-Werten funktioniert bei NF und IP nicht. Die maßgeblichen Formeln verwenden die Multiplikation und Division von linearen Verstärkungs- und Leistungswerten, wobei zuerst dB und / oder dBm in lineare Zahlen (Verstärkungsverhältnis und mW) unter Verwendung von Antilogs konvertiert werden müssen, die Kaskadenberechnungen durchgeführt werden müssen und das Ergebnis dann wieder in dB und / oder zurück konvertiert werden muss. oder dBm mit Protokollen.

Nicht alle Systemkaskadenvorgänge erfordern eine Konvertierung hin und her. Wenn beispielsweise nur die Gesamtverstärkung und / oder der Ausgangsleistungspegel des Systems benötigt werden, können Berechnungen entweder mit linearen Einheiten (mW und Multiplikatoren) oder logarithmischen Einheiten (dBm bzw. dB) durchgeführt werden.

Die Definition von 'dB' und 'dBm'

Ein Dezibel (dB) in der Elektrotechnik ist definiert als 10-mal der Basis-10-Logarithmus eines Verhältnisses zwischen zwei Leistungsstufen; zB Pout / Pin (mit anderen Worten Gain). Nämlich:

Alle Gewinne größer als 1 werden daher als positive Dezibel (> 0) ausgedrückt, und Gewinne kleiner als 1 werden als negative Dezibel (<0) ausgedrückt. Beachten Sie, dass in den meisten Fällen das lineare Verhältnis von P1 / P2 eine positive Zahl (> 0) sein muss, da der Logarithmus von 0 undefiniert ist und der Logarithmus der negativen Zahlen komplex ist (sie enthalten sowohl einen Real- als auch einen Imaginärteil ). Der dB-Wert kann jedoch theoretisch jeden Wert zwischen −∞ und + ∞ annehmen, einschließlich 0, was einer Verstärkung von 1 entspricht [10 * log (1) = 0 dB].

'dBm' ist eine auf Dezibel basierende Leistungseinheit, die sich auf 1 mW bezieht. Da die Verstärkung von 0 dB gleich der Verstärkung von 1 ist, ist die Leistung von 1 mW um 0 dB größer als 1 mW oder 0 dBm. In ähnlicher Weise ist eine Leistungseinheit von dBW relativ zu 1 W Leistung dezibel.


Dementsprechend sind alle dBm-Werte größer als 0 größer als 1 mW und alle dBm-Werte kleiner als 0 kleiner als 1 mW (siehe Abb. 1). Beispielsweise ist + 3.01 dBm 3.01 dB größer als 1 mW; dh oder 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). - 3.01 dBm ist 3.01 dB weniger als 1 mW; dh oder 0 dBm + (-3.01) dB = -3.01 dBm (0.5 mW).

Die folgende Tabelle enthält einige numerische Beispiele, damit Sie die Korrelation zwischen mW und dBm sehen können. Derselbe Satz von Werten, der auf einer logarithmischen Skala aufgetragen ist, würde eine gerade Linie erzeugen. Aufgrund der logarithmischen Beziehung werden in der Grafik die kleineren Werte gegen die linke vertikale Achse gebündelt. Eine vergrößerte Version des 0-zu-1-MW-Bereichs ist der Übersichtlichkeit halber eingefügt.

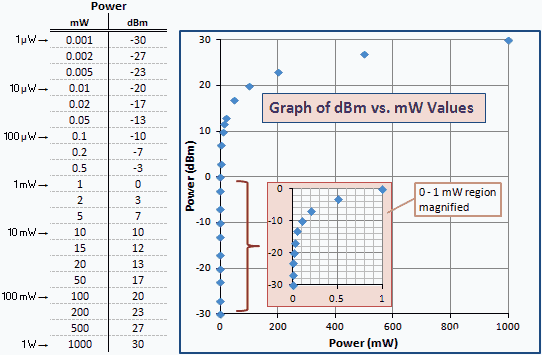
Abb. 1 - Leistungsdiagramm in dBm gegen mW

Fig. 2 ist eine Tabelle und ein Diagramm von dB gegenüber linearen Verstärkungsverhältnissen ähnlich dem dBm gegenüber mW in Fig. 1. Beachten Sie, dass die Zahlen und Kurven genau gleich sind. Nur die Achsenbeschriftungen werden geändert. Dies liegt daran, dass dBm eine Leistungseinheit ist, die in dB relativ zu 1 mW (0 dBm) ausgedrückt wird.

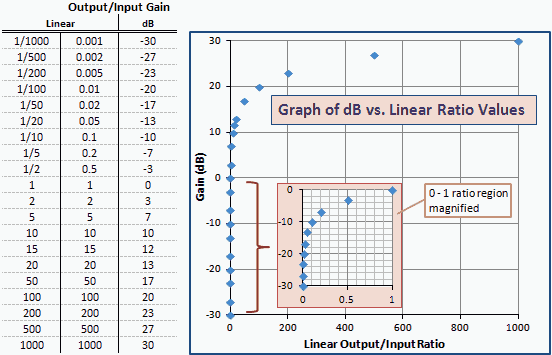
Abb. 2 - Diagramm der Verstärkung in dBm gegenüber dem linearen Verhältnis

Grundsätzlich ist Gewinn ein Multiplikations- (oder Divisions-) Faktor. Beispielsweise kann ein Verstärker eine Verstärkung haben, die das Signal von Eingang zu Ausgang um den Faktor 4 (dh 4x) erhöht (siehe Abb. 3). Wenn ein 1 mW-Signal (0 dBm) in den Verstärker eingespeist wird, wird 1 mW * 4 = 4 mW ausgegeben. In Dezibel ausgedrückt entspricht ein Faktor von 4 10 * log (4) = 6.02 dB, dh 0 dBm plus 6.02 dB Verstärkung ergibt + 6.02 dBm am Ausgang.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

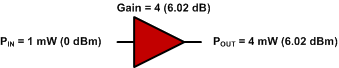
Abb. 3 - Verstärkung einzelner Verstärker.

Kombinieren von Gains (linear und dB) mit positivem Wert

Wenn ein Verstärker mit einer Verstärkung von 4 in Reihe mit einem zweiten Verstärker mit einer Verstärkung von 6 geschaltet ist, ist die Gesamtverstärkung 4 * 6 = 24. In Dezibel ausgedrückt entspricht ein Faktor von 6 10 * log (6) = 7.78 dB und ein Faktor von 24 10 * log (24) = 13.8 dB.

Genau wie 4 x 6 = 24 (lineare Verstärkung) ist 6.02 dB + 7.78 dB = 13.8 dB (Dezibel-Verstärkung).

Wenn ein 1 mW-Signal (0 dBm) in den Verstärker eingespeist wird, kommt 4 mW aus dem ersten Verstärker und 24 mW aus dem zweiten Verstärker. Siehe Abb. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Abb. 4 - Kaskadierte Doppelverstärkerverstärkung.

Gewinn und Verlust kombinieren (linear und dB)
Dieses nächste Beispiel zeigt, was passiert, wenn eine Verstärkung <1 (ein Verlust) auftritt, bei der ein Dämpfungsglied mit einer Verstärkung von 1/6 nach dem ersten Verstärker platziert wird, anstatt einen zweiten Verstärker zu haben. Siehe Abb. 5.
4 * 1 / 6 = 2 / 3 (lineare Verstärkung). In ähnlicher Weise ist 6.02 dB - 7.78 dB = - 1.76 dB (Dezibel-Verstärkung).
Wenn wie im vorherigen Beispiel ein 1 mW-Signal (0 dBm) mit einer Verstärkung von 4 in den Verstärker eingespeist wird, wird 4 mW ausgegeben. Dieser 4 mW geht dann mit einer linearen Verstärkung von 1 / 6 in den Abschwächer und wird mit einer Leistung von 4 / 6 mW (2 / 3 mW) ausgegeben.
Die Gesamtverstärkung beträgt in diesem Fall 4 / 6 = 2 / 3, sodass die Ausgangsleistung tatsächlich geringer ist als die Eingangsleistung.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = -1.76 dBm

Abb. 5 - Kaskadierte Verstärkung und Dämpfung.

12 mW + 34 mW + 8 mW + 20 dB

Ergänzende Informationen zu Logarithmen
Logarithmen von Produkten
Eine implizit oben verwendete Eigenschaft von Logarithmen gibt Folgendes an und ist die Grundlage dafür, dass Logarithmuswerte addiert und subtrahiert werden können, anstatt ihre linearen Äquivalente zu multiplizieren.

'h * j / k * m / n' könnte eine Kaskade von Komponenten darstellen, die drei Geräte (h, j und m) mit jeweils einer Verstärkung> 1 und zwei Geräte (k und n) mit jeweils einer Verstärkung <1 aufweisen (siehe Fig. 6). Die Gesamtsystemverstärkung kann entweder durch Multiplizieren aller linearen Verstärkungswerte oder durch Addieren aller Dezibelverstärkungswerte berechnet werden.

Abb. 6 - Kaskadierte Komponenten

Logarithmen der Exponenten
Das Folgende ist wichtig, um zu verstehen, warum die Leistungsverstärkung in Bezug auf die Leistung 10 * log (Pout / Pin) dB beträgt, während die Leistungsverstärkung in Bezug auf die Spannung 20 * log (Vout / Vin) dB beträgt.


Das ist so, weil cf gleich c ist multipliziert mit sich selbst 'f' mal. Zum Beispiel, wenn f = 4:


Leistungssteigerung basierend auf Leistung vs. Leistungssteigerung basierend auf Spannung
Die Leistungsverstärkung ist Pout / Pin und die Spannungsverstärkung ist Vout / Vin. Die auf einem Leistungsverhältnis in Dezibel basierende Leistungsverstärkung wird als 10 * log (Pout / Pin) definiert. Die Spannungsverstärkung beträgt [(Vout2 / R) / (Vin2 / R)], da gemäß dem Ohmschen Gesetz P = V2 / R. Das 'R' in den Nennern hebt das Verlassen von Vout2 / Vin2 auf, was gleich (Vout / Vin) 2 ist, wie durch die Exponentenregel definiert, die lautet ac / bc = (a / b) c. Daher:

Wichtige Notiz: Die Spannungsverstärkung in Bezug auf die Spannung beträgt 10 * log (Vout / Vin) dB, genau wie bei der Leistungsverstärkung in Bezug auf die Leistung. Nur wenn die Leistungsverstärkung als Spannung ausgedrückt wird, gilt die 20 * log (Vout / Vin) dB-Gleichung. Dies ist ein häufiger Punkt der Verwirrung.


Keine Operation in der Mathematik ist willkürlich, und deshalb wird ein Signalleistungsverlust (Verstärkung <1) als negativer Wert dargestellt und daher während einer Kaskadenberechnung subtrahiert. Es ist eine einfache Demonstration, aber erwähnenswert.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

Wenn Sie einen Radiosender bauen möchten, verstärken Sie Ihren UKW-Radiosender oder benötigen Sie einen anderen UKW-Ausrüstung, Sie können uns gerne kontaktieren: [E-Mail geschützt] .

Hinterlass eine Nachricht 

Nachrichtenliste