Leistung und Amplitude: Watt, Volt und Bezugsdezibel

Einleitung
In Hochfrequenzanwendungen (aber auch in vielen anderen Anwendungen) ist es sehr verbreitet, mit sehr großen und sehr kleinen Signalen umzugehen. Beispielsweise kann ein Transceiver eine Leistung von 100 W senden und nur 10 fW (oder 0.000'000'000'000'01'1 W) empfangen. Diese extrem unterschiedlichen Leistungspegel können sich die gleichen Schaltkreise teilen. Natürlich können diese Zahlen in Watt mit der technischen Notation (wie oben) oder mit der wissenschaftlichen Notation ausgedrückt werden, wie 102 · 1 W und 10 · 14 – XNUMX W, aber sie sind ziemlich schwer auszusprechen und wenn der Exponent falsch geschrieben ist wird der resultierende Fehler sehr groß sein.

Eine andere Möglichkeit besteht darin, den Logarithmus zu verwenden und alle Leistungen in dBm umzurechnen. 100 W wird zu + 50 dBm und 10 fW wird zu –110 dBm: Diese Zahlen sind auswendig leichter zu handhaben und leichter zu schreiben. Wenn dann die Dämpfung und die Verstärkung verschiedener Schaltungsblöcke auch in dB ausgedrückt werden, kann man zur Ermittlung der endgültigen Leistung einfach alles addieren, anstatt zu multiplizieren, was die Berechnungen weiter vereinfacht.

Nicht jeder ist mit dB, dBm und ähnlichen (Pseudo-) Einheiten vertraut: Sie müssen nicht unbedingt verwendet werden, sind jedoch in der Technik so weit verbreitet, dass es sehr schwierig ist, sie zu vermeiden.

Eine Theorie
Dezibel (dB) werden verwendet, um Leistungsverhältnisse logarithmisch auszudrücken, so dass sehr große und sehr kleine Leistungen mit komfortablen Zahlen verglichen werden können. Ein Dezibel ist eine dimensionslose Pseudoeinheit, da es durch das Verhältnis zweier Potenzen definiert ist. Da Dezibel jedoch so praktisch sind, dass sie wahre Potenz anstelle eines dimensionslosen Verhältnisses ausdrücken, werden sehr häufig Dezibel verwendet, auf die verwiesen wird.

Wenn wir über Leistung sprechen, definiert die folgende Gleichung den Leistungspegel P in dB der Leistung p in W, bezogen auf die Leistung p0:

Der 10-Faktor ist, weil Dezibel "Zehntel der Glocken" sind. Aber ich habe noch nie von einer Messung in Bells gehört, es werden nur Dezibel verwendet.

Die gebräuchlichste Einheit ist der dBm (sprich "dBm"), der auch als dBmW oder Dezibel-Milliwatt bezeichnet wird. Dies ist nur der Leistungspegel in dB im Vergleich zu einer Referenzleistung von p0 = 1 mW. Manchmal werden auch dBW verwendet und sie drücken das Leistungsverhältnis relativ zu p0 = 1 W aus, aber sie sind nicht sehr verbreitet.

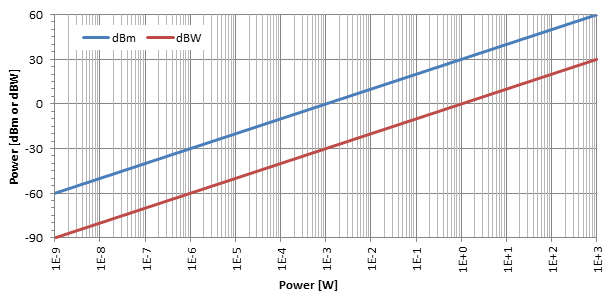
Wie im obigen Diagramm gezeigt, ist der logarithmische Effekt der Dezibelumwandlung ziemlich offensichtlich. Wie man auf diesem Log-Lin-Plot sehen kann, sind dBm und dBW nur ​​zwei durch 30 dB getrennte gerade Linien: Um dBm in dBW zu konvertieren, subtrahieren Sie einfach 30.

In einigen Bereichen, wie dem analogen TV-Empfang, wird häufig die Spannung anstelle der Leistung gemessen. Dies ist kein Problem, solange die Impedanz bekannt und festgelegt ist (Fernsehempfänger verwenden normalerweise 75 Ω).

Absolute Spannungen können auch die logarithmische Dezibel-Skala nutzen, indem Dezibel-Mikrovolt (dBμV) und Dezibel-Volt (dBV) verwendet werden. Am gebräuchlichsten sind dBμV, die das Spannungsverhältnis zu u0 = 1 μV ausdrücken. Manchmal werden auch dBV verwendet und drücken das Spannungsverhältnis zu u0 = 1 V aus.

Beachten Sie, dass die Spannungen in ihrer dB-Formel einen "20" anstelle eines "10" verwenden. Dies liegt daran, dass Dezibel immer als Leistungsverhältnisse definiert sind. Wenn wir nur Spannungen haben, müssen wir diese zuerst quadrieren, um die Leistung zu finden. Diese Zweierpotenz multipliziert den vorhandenen Faktor von 10 mit 2, wenn sie aus dem Logarithmus herausgenommen wird.

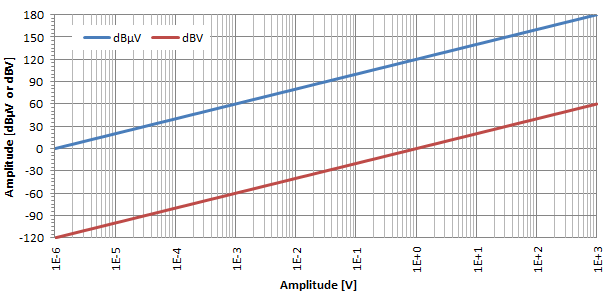
Wie im obigen Diagramm und auf ähnliche Weise wie zuvor gezeigt, ist der logarithmische Effekt der Dezibelumwandlung auch für Spannungen ziemlich offensichtlich. Wie man auf diesem Log-Lin-Plot sehen kann, sind dBμV und dBV nur zwei durch 120 dB getrennte gerade Linien: Um dBμV in dBV zu konvertieren, subtrahieren Sie einfach 120.

Wenn wir nun von Strom in Spannung und umgekehrt konvertieren möchten, müssen wir die Impedanz kennen. Wir verwenden nur die folgende Gleichung:

Diese Umwandlung ist nur gültig, wenn die Impedanz Zc real ist und die Last an die Übertragungsleitung angepaßt ist.

Wenn wir den Leistungspegel in dBm und den Amplitudenpegel in dBμV als Funktion der Leistung in W für eine gegebene Impedanz (hier Zc = 50 Ω) zeichnen, erhalten wir Folgendes:

Wie zuvor haben wir zwei parallele Linien, die 107 dB voneinander entfernt sind. Für die Umrechnung von dBm in dBμV addieren Sie einfach 107 dB für Zc = 50 Ω, 109 dB für Zc = 75 Ω, 115 dB für Zc = 300 Ω oder 118 dB für Zc = 600 Ω.

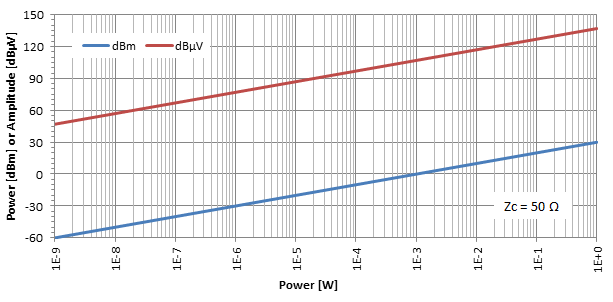
Praktische Überlegungen
Auf den ersten Blick mag man meinen, dass wegen des Logarithmus ein Taschenrechner unbedingt notwendig ist, um mit dBm umzugehen. Tatsächlich kann eine grobe Berechnung leicht in Ihrem Kopf durchgeführt werden. Sie müssen sich nur drei Fakten merken:
 Eine Leistung von 1 mW ist 0 dBm.
 Addieren Sie jedes Mal, wenn sich die Leistung verdoppelt, 3 dB.
 Addieren Sie jedes Mal, wenn sich die Leistung um den Faktor 10 erhöht, 10 dB.

Betrachten wir nun einige Beispiele: Nehmen wir an, wir haben einen Leistungspegel von 26 dBm. Wir können 26 dBm = 0 dBm + 10 dB + 10 dB + 3 dB + 3 dB schreiben, und mit den vorherigen drei einfachen Regeln können wir die Leistung leicht finden, indem wir 1 mW · 10 · 10 · 2 · 2 = 400 mW .

Ein weiteres Beispiel: Angenommen, wir haben -33dBm: Wir können schreiben als -33 dBm = 0 dBm - 10 dB - 10 dB - 10dB - 3 dB, und wir finden 1 mW / 10 / 10 / 10 / 2 = 0.5 μW.

Dies funktioniert auch umgekehrt, zum Beispiel sind 50 mW nur ​​1 mW · 10 · 10 / 2. In dBm haben wir 0 dBm + 10 dB + 10 dB –3 dB = 17 dBm.

Dies erfordert etwas Übung, ist aber sehr einfach zu bewerkstelligen. Es ist nicht so genau wie ein Taschenrechner, weil Sie nur mit ± 2 dB genau sein können, aber für den Aufwand eine sehr gute Vorstellung von der Stärke eines Signals geben.

Eine ähnliche Methode funktioniert auch für dBμV, die Regeln sind jedoch unterschiedlich:
 Eine Amplitude von 1 μV ist 0 dBμV.
 Addieren Sie jedes Mal, wenn sich die Amplitude verdoppelt, 6 dB.
 Addieren Sie jedes Mal, wenn sich die Amplitude um den Faktor 10 erhöht, 20 dB.

Sie werden überrascht sein über die Berechnungen in Dezibel, die zuvor gezeigt wurden, wobei dB zu dBm addiert werden, was ziemlich seltsam ist. Dies liegt daran, dass Dezibel Pseudoeinheiten sind und sich nicht wie gewohnt verhalten. Das Verhältnis zweier Leistungen wird in dB ausgedrückt, ist jedoch dimensionslos: Beispielsweise bedeutet 3 dB nur "doppelt so viel". Die in dBm ausgedrückte Leistung ist tatsächlich eine Leistung: Beispielsweise bedeutet 10 dBm "10 mal stärker als 1 mW", was 10 mW bedeutet.

Wenn Sie nun Dezibel (dB, dBm, ...) addieren, multiplizieren Sie die ursprünglichen Zahlen aufgrund ihrer logarithmischen Natur. Wenn Sie also eine Verstärkung von 3 dB zu einer Leistung von 10 dBm hinzufügen, erhalten Sie 13 dBm. Aber was Sie wirklich getan haben, ist das Multiplizieren eines Faktors von 2 mit einer Leistung von 10 mW, um 20 mW zu erhalten, was 13 dBm ist!

So weit so gut, ist das Hinzufügen im Kopf viel einfacher als das Multiplizieren, und das macht Dezibel so praktisch. Aber es gibt ein Problem: Da das Addieren von Dezibel dem Multiplizieren der ursprünglichen Faktoren entspricht, wie kann man die Potenz zweier Signale addieren (kombinieren)? Das kannst du nicht. Sie können dBm nicht zu dBm hinzufügen. Wenn Sie zum Beispiel eine Schaltung oder ein Gerät haben, das die Leistung eines Signals von 10 dBm (10 mW) mit der Leistung eines anderen Signals von 13 dBm (20 mW) kombiniert, ist das Ergebnis 10 mW + 20 mW = 30 mW ist 14.8 dBm. Dies ist nicht direkt in dBm möglich. Sie müssen beide Leistungen in Watt umrechnen, addieren und in dBm zurückrechnen. Dies ist eine große Einschränkung der Dezibel und eine häufige Gefahr. Zum Glück ist diese Operation nicht sehr verbreitet.

Wenn Sie einen Radiosender bauen möchten, verstärken Sie Ihren UKW-Radiosender oder benötigen Sie einen anderen UKW-Ausrüstung, Sie können uns gerne kontaktieren: [E-Mail geschützt] .

Hinterlass eine Nachricht 

Nachrichtenliste